Các đường trong tam giác - Cách giải nhanh tọa độ Oxy
Khám phá toàn tập các đường trong tam giác từ lý thuyết cơ bản đến phương pháp giải nhanh tọa độ Oxy. Hướng dẫn lập phương trình đường cao, trung tuyến và mẹo tìm tọa độ H, G.
Trong hình học, các đường đặc biệt trong tam giác không chỉ là những đường kẻ đơn thuần mà chúng là "linh hồn" của mọi bài toán chứng minh và tọa độ. Việc làm chủ các đường này không chỉ giúp bạn giải toán nhanh hơn mà còn xây dựng một tư duy logic chặt chẽ.
Tổng hợp 5 đường trong tam giác
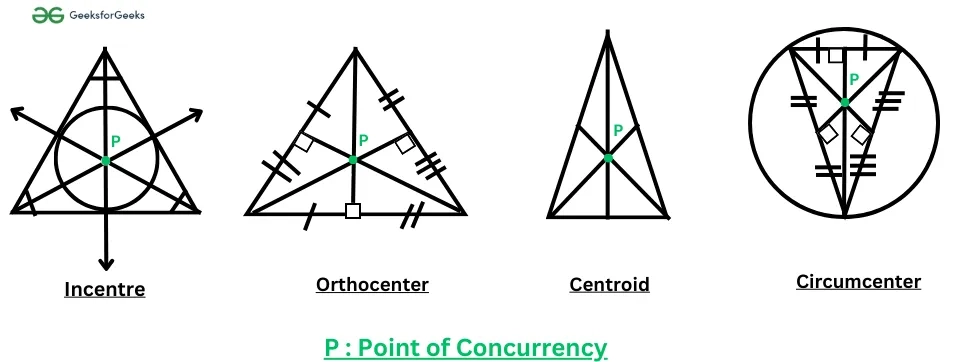
Trong một tam giác, chúng ta có 5 loại đường cốt lõi dẫn đến các điểm đồng quy đặc biệt. Đây là những "điểm chạm" quan trọng trong mọi đề thi:
- Đường trung tuyến: Nối từ đỉnh đến trung điểm của cạnh đối diện. Ba đường trung tuyến giao nhau tại Trọng tâm $G$.
- Đường cao: Đường thẳng đi qua đỉnh và vuông góc với cạnh đối diện. Ba đường cao giao nhau tại Trực tâm $H$.
- Đường trung trực: Đường thẳng đi qua trung điểm và vuông góc với cạnh đó. Ba đường trung trực giao nhau tại Tâm đường tròn ngoại tiếp $O$.
- Đường phân giác: Đường thẳng chia đôi góc ở đỉnh thành hai góc bằng nhau. Ba đường phân giác giao nhau tại Tâm đường tròn nội tiếp $I$.
- Đường trung bình: Đoạn thẳng nối trung điểm của hai cạnh. Nó song song và bằng một nửa cạnh thứ ba.
Cách lập phương trình các đường trong tam giác trên mặt phẳng tọa độ $Oxy$
Khi chuyển sang đại số hóa hình học, mỗi loại đường sẽ có một "bí kíp" lập phương trình riêng dựa trên hai yếu tố: điểm đi qua và vectơ.
- Đường cao (đi qua $A$): Nhận vectơ $\vec{BC} = (x_C - x_B; y_C - y_B)$ làm vectơ pháp tuyến $\vec{n}$. Phương trình có dạng tổng quát: $a(x - x_A) + b(y - y_A) = 0$.
- Đường trung tuyến (đi qua $A$ và trung điểm $M$ của $BC$): Trước tiên, tìm tọa độ $M$:
$$M = \left( \frac{x_B + x_C}{2}; \frac{y_B + y_C}{2} \right)$$
Sau đó, viết phương trình đường thẳng đi qua hai điểm $A$ và $M$. - Đường trung trực (cạnh $BC$): Nhận vectơ $\vec{BC}$ làm vectơ pháp tuyến và đi qua trung điểm $M$ của $BC$.
Phương pháp tìm tọa độ Trực tâm $H$ và trọng tâm $G$ bằng hệ phương trình
Trong phòng thi, thời gian là vàng bạc. Thay vì vẽ hình phức tạp, hãy sử dụng sức mạnh của đại số để tìm tọa độ các điểm này.
- Tìm Trọng tâm $G$: Đây là điểm dễ tìm nhất. Bạn chỉ cần lấy trung bình cộng tọa độ của 3 đỉnh:
$$G = \left( \frac{x_A + x_B + x_C}{3}; \frac{y_A + y_B + y_C}{3} \right)$$
- Tìm Trực tâm $H$: Giả sử $H(x; y)$. Vì $H$ là trực tâm, ta có hệ điều kiện vuông góc thông qua tích vô hướng bằng 0:
$$\begin{cases} \vec{AH} \cdot \vec{BC} = 0 \\ \vec{BH} \cdot \vec{AC} = 0 \end{cases}$$
Giải hệ phương trình bậc nhất hai ẩn này, bạn sẽ tìm được tọa độ chính xác của $H$.
Bí quyết viết phương trình đường trung trực và tìm tâm đường tròn ngoại tiếp tam giác
Tâm đường tròn ngoại tiếp $O$ chính là giao điểm của các đường trung trực. Tuy nhiên, nếu bạn không muốn lập phương trình đường thẳng, hãy dùng "tuyệt chiêu" khoảng cách.
Cách 1 (Giao điểm): Lập phương trình hai đường trung trực của hai cạnh (ví dụ $AB$ và $AC$), sau đó tìm giao điểm của chúng.
Cách 2 (Sử dụng bán kính $R$): Giả sử $O(x; y)$. Vì $O$ cách đều 3 đỉnh nên $OA = OB = OC$. Ta có hệ phương trình:
$$\begin{cases} OA^2 = OB^2 \\ OA^2 = OC^2 \end{cases}$$
Khi khai triển các biểu thức bình phương khoảng cách, các hạng tử $x^2$ và $y^2$ sẽ tự triệt tiêu, để lại cho bạn một hệ phương trình bậc nhất cực kỳ đơn giản để giải.
Hy vọng bài viết này đã giúp bạn "giải mã" được sự phức tạp của các đường trong tam giác. Việc kết hợp giữa tư duy hình học trực quan và kỹ thuật tọa độ đại số chính là chìa khóa để bạn đạt điểm tối đa trong các kỳ thi sắp tới.
>>> Xem thêm:
- Hệ thống kiến thức về tính chất ba đường cao của tam giác
- Lý thuyết tính chất ba đường trung trực của tam giác
Bài Viết Liên Quan
Tác giả Phương Mai – Người truyền lửa tại toanhoc.edu.vn. Với chuyên môn Toán học chuyên sâu, cô chia sẻ kiến thức tư duy logic và phương pháp giải toán sáng tạo giúp học sinh làm chủ mọi con số.