Đường tròn không chỉ là một hình học phẳng hoàn hảo mà còn là nền tảng quan trọng trong các bài toán quỹ đạo, lượng giác và thậm chí là ứng dụng trong các phân phối xác suất hình học. Với góc độ sư phạm, bài viết này sẽ giúp bạn hệ thống lại kiến thức một cách logic và "bắt bài" những lỗi sai thường gặp nhất.
Định nghĩa đường tròn và các yếu tố cơ bản
Trong mặt phẳng, đường tròn tâm $O$ bán kính $R$ (ký hiệu là $(O; R)$) là tập hợp tất cả các điểm cách điểm $O$ một khoảng cố định bằng $R$.
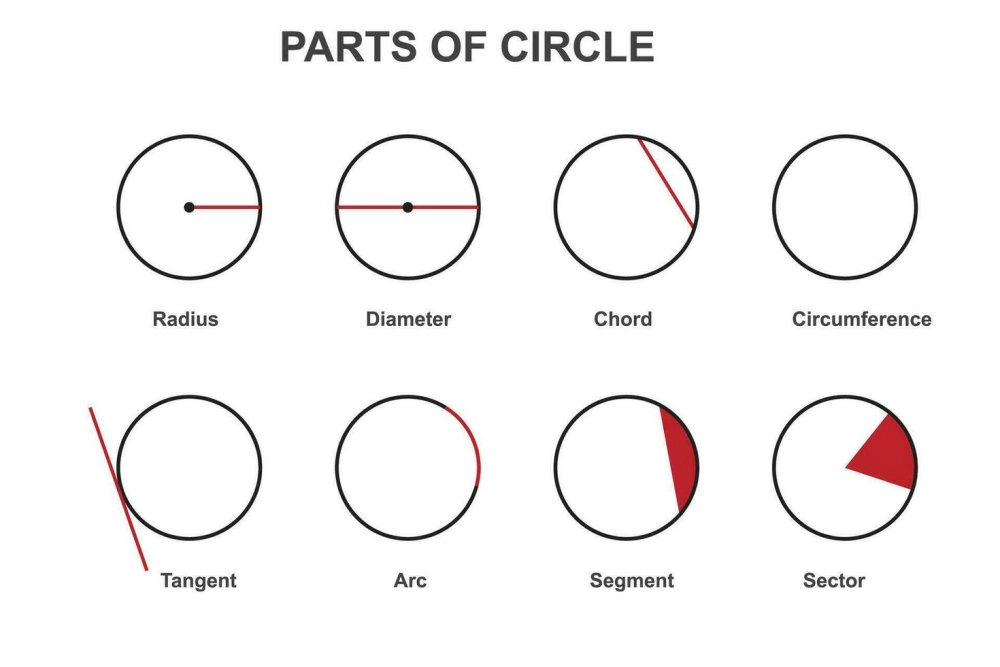
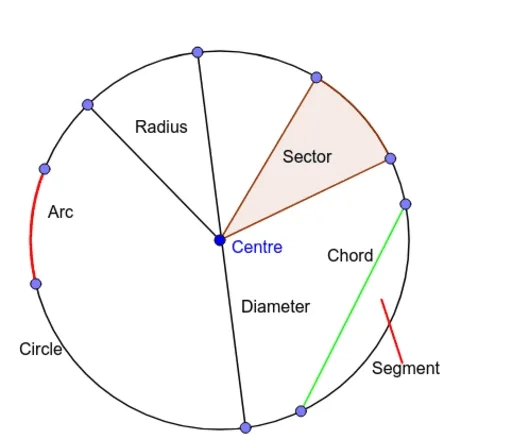
Các yếu tố cốt lõi bạn cần nắm vững:
- Tâm ($O$): Điểm cố định nằm chính giữa.
- Bán kính ($R$): Đoạn nối từ tâm đến một điểm bất kỳ trên đường tròn.
- Dây cung: Đoạn thẳng nối hai điểm bất kỳ trên đường tròn.
- Đường kính ($d$): Dây cung đi qua tâm, có độ dài $d = 2R$.
Mẹo SEO & Ghi nhớ: Hãy coi đường tròn như một tập hợp các điểm thỏa mãn phương trình chính tắc trong hệ tọa độ $Oxy$:
$$(x - a)^2 + (y - b)^2 = R^2$$
Trong đó $(a, b)$ là tọa độ tâm $O$. Đây là nền tảng để giải các bài toán tương quan vị trí sau này.
Tính chất đối xứng và vị trí tương đối giữa điểm, đường thẳng với đường tròn
Tính chất đối xứng
Đường tròn là hình có độ đối xứng hoàn hảo:
- Đối xứng tâm: Tâm $O$ là tâm đối xứng.
- Đối xứng trục: Bất kỳ đường thẳng nào đi qua tâm cũng là trục đối xứng.
Vị trí tương đối
Để xác định vị trí, ta so sánh khoảng cách $d$ từ điểm/đường thẳng tới tâm $O$ với bán kính $R$.
Đối tượng | Điều kiện | Vị trí tương đối |
Điểm $M$ | $OM < R$ | $M$ nằm trong đường tròn |
$OM = R$ | $M$ nằm trên đường tròn | |
$OM > R$ | $M$ nằm ngoài đường tròn | |
Đường thẳng $\Delta$ | $d(O, \Delta) < R$ | Cắt đường tròn tại 2 điểm (Cát tuyến) |
$d(O, \Delta) = R$ | Tiếp xúc với đường tròn (Tiếp tuyến) | |
$d(O, \Delta) > R$ | Không giao nhau |
Quan hệ giữa đường kính và dây cung trong đường tròn
Đây là phần "xương sống" để giải quyết các bài toán tính toán độ dài và chứng minh vuông góc.
- Đường kính vuông góc với dây cung: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
- Đường kính đi qua trung điểm dây cung: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Sai lầm cần tránh: Rất nhiều học sinh quên điều kiện "dây không đi qua tâm" ở định lý 2. Nếu dây là đường kính, nó luôn đi qua trung điểm (là tâm) nhưng không nhất thiết phải vuông góc với các đường kính khác.
Công thức giải nhanh: Gọi $h$ là khoảng cách từ tâm đến dây cung có độ dài $AB$, ta luôn có mối liên hệ Py-ta-go:
$$R^2 = h^2 + \left(\frac{AB}{2}\right)^2$$
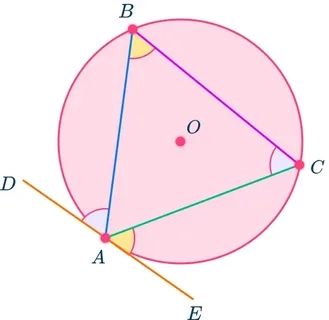
Tính chất của tiếp tuyến và hai tiếp tuyến cắt nhau
Tiếp tuyến là đường thẳng chỉ "chạm" đường tròn tại một điểm duy nhất (tiếp điểm).
Tính chất cơ bản
Nếu đường thẳng $d$ là tiếp tuyến của $(O)$ tại điểm $A$ thì $OA \perp d$.
Tính chất hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn $(O)$ cắt nhau tại một điểm $M$ (với $A, B$ là các tiếp điểm), ta có:
- $MA = MB$ (Đoạn thẳng nối từ điểm cắt đến hai tiếp điểm bằng nhau).
- $MO$ là tia phân giác của góc $\angle AMB$.
- $OM$ là tia phân giác của góc $\angle AOB$.
Tính chất này thường xuất hiện trong các bài toán xác suất hình học khi tính miền diện tích thỏa mãn điều kiện tiếp xúc, hoặc trong các cấu trúc kỹ thuật như ròng rọc và dây curoa.
Hy vọng bài viết giúp bạn hệ thống kiến thức vững chắc. Hãy luyện tập thêm các dạng toán phối hợp để tối ưu điểm số. Bạn có muốn tôi thiết kế thêm một bài kiểm tra trắc nghiệm 10 câu để tự ôn luyện không?
>>> Xem ngay bài viết:
Lý thuyết góc có đỉnh ở bên ngoài đường tròn - Toán lớp 9
Định nghĩa góc có đỉnh ở bên trong đường tròn
